3DOscillo1 from Mauno Tuominen on Vimeo.
sunnuntai 21. joulukuuta 2014
3D-oscilloscope interface
I have a great book "Design Techniques for Electronics Engineers" from McGraw-Hill publications. In this book there is one very simple circuit that adds diagonal axis (Z-axis) to any normal dual-channel oscilloscope that can display X/Y lissajous figures. I decided that this is a good project to end this year. Pictured is my design of this circuit in Euro-modular format and the circuit schematics. There are three inputs with attenuator pots and X/Y-output to the oscilloscope. For 3D-effect the Z-input is applied simultaneously to both the X and Y inputs (amplifiers IC1B and IC1C). Gains through these amplifiers are also adjustable with trimmers to vary the angle of perspective. Here is also a short video to show you what this means in practice. I have connected three different VCOs to the inputs. In this video I adjust the phase between X and Y VCOs and the frequency/wave-shape of all VCOs. I do not yet know if there are any musical applications for this module. The sound from the X/Y-output is not so interesting. If I use the output for modulation purposes I could maybe get more interesting musical results. But the figures that you can generate on oscilloscope are fascinating, much fun for Christmas evenings !
3DOscillo1 from Mauno Tuominen on Vimeo.
3DOscillo1 from Mauno Tuominen on Vimeo.
perjantai 12. joulukuuta 2014
Rob Hordijk's Twin Peak Filter Simulation
Rob Hordijk presented an interesting masterclass in Sines And Squares Festival 2014:
http://vimeo.com/111250081
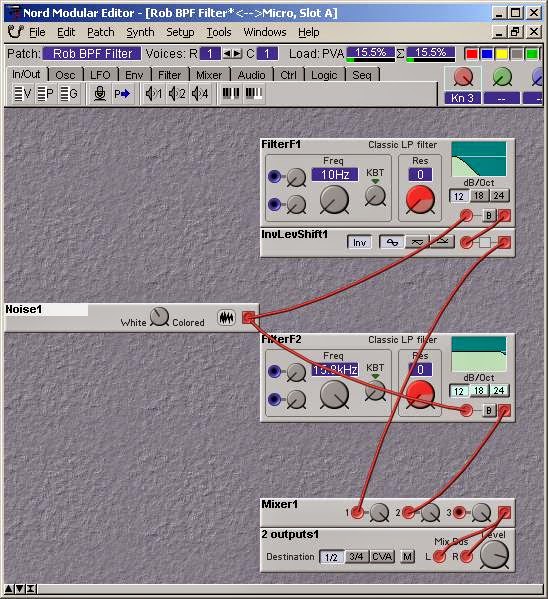
At 10:00 of this Part-2 Video Rob starts to talk about his Twin Peak Filter. It is an interesting solution for band-pass filter. You connect two low-pass filters parallel and subtract the output of the one filter from the output of the other one. This works if the gain of the both LP filters is always equal. I decided to try this with MicroModulars classic LP filters. Filters are in 12dB/Oct mode and one filter output is inverted (F2-F1) before they are summed in mixer. I defined a morph group for resonance (max resonance is limited so that the filters are just not oscillating) of the both filters and assigned a knob to control resonance. This assures that the resonance and the gain of the both filters is equal. Pictured is the test-patch of this filter and a picture that shows the different filter topologies you can get out of this patch when you alter the cutoff frequencies of the LP filters.
In dual band pass mode when you dial equal frequencies to F1 and F2 the sound disappears and there is only silence (F2-F1=0). You can get the idea of Rob's filter easily from this emulation. It doesn't sound bad ;)
http://vimeo.com/111250081
At 10:00 of this Part-2 Video Rob starts to talk about his Twin Peak Filter. It is an interesting solution for band-pass filter. You connect two low-pass filters parallel and subtract the output of the one filter from the output of the other one. This works if the gain of the both LP filters is always equal. I decided to try this with MicroModulars classic LP filters. Filters are in 12dB/Oct mode and one filter output is inverted (F2-F1) before they are summed in mixer. I defined a morph group for resonance (max resonance is limited so that the filters are just not oscillating) of the both filters and assigned a knob to control resonance. This assures that the resonance and the gain of the both filters is equal. Pictured is the test-patch of this filter and a picture that shows the different filter topologies you can get out of this patch when you alter the cutoff frequencies of the LP filters.
In dual band pass mode when you dial equal frequencies to F1 and F2 the sound disappears and there is only silence (F2-F1=0). You can get the idea of Rob's filter easily from this emulation. It doesn't sound bad ;)
tiistai 9. joulukuuta 2014
LED Beat Frequency Video
LED Beat Frequency module is ready and working. Pictured is the new
version with FlatKeys FK50240 top octave generator. Right side is the
2MHz crystal clock that is divided by 16 with 4520-counter to get the
440Hz A. Left side is the LED Beat Frequency circuit that I found here: www.tradeofic.com/Circuit/3962-HI_L0_LED_FREQUENCY_DISPLAY.html
I changed it to CMOS-logic and added a 4.7k resistor from NPN-transistors (2N3904) collector to +12V. Both the reference and external inputs have this transistor circuit. I also added output-jack for the reference frequency so this module can also be used as a traditional tuning-reference. The video shows this module in action. L-channel is the tuning reference and R-channel is the external VCO that is tuned. First I switch the tuning reference to C. Then I tune the external VCO to unison. After this I tune the external VCO to perfect fifth G (notice the different LED-beat pattern). Then I tune the VCO to perfect octave. If you look at the LED's carefully you can also tune to other intervals but unison, perfect fifth and the octaves are the easiest. Notice also how the LED's show precisely the slow beating of the frequencies when tuning is almost done.
BeatFreq1 from Mauno Tuominen on Vimeo.
I changed it to CMOS-logic and added a 4.7k resistor from NPN-transistors (2N3904) collector to +12V. Both the reference and external inputs have this transistor circuit. I also added output-jack for the reference frequency so this module can also be used as a traditional tuning-reference. The video shows this module in action. L-channel is the tuning reference and R-channel is the external VCO that is tuned. First I switch the tuning reference to C. Then I tune the external VCO to unison. After this I tune the external VCO to perfect fifth G (notice the different LED-beat pattern). Then I tune the VCO to perfect octave. If you look at the LED's carefully you can also tune to other intervals but unison, perfect fifth and the octaves are the easiest. Notice also how the LED's show precisely the slow beating of the frequencies when tuning is almost done.
BeatFreq1 from Mauno Tuominen on Vimeo.
LED Beat Frequency Project
This is an old-and-new project. I wanted to
build a tuning reference with visual feedback. This allows me to make
some crazy non-melodic stuff with VCOs and after that some melodic lines
that are in specific musical key without listening the
VCO. The display circuit takes two inputs (f1,f2) and displays the
difference frequency between these two frequencies with four LEDs
arranged in a circle. Only one LED conducts at a time so what is
displayed is a dot of light. The dot rotates clockwise when f1 is
greater than f2 and counterclockwise when f1 is smaller. The rate of
rotation is the beat frequency between f1 and f2. When f1 equals f2, the
dot remains stationary. Originally I generated the reference frequency
f1 with XR2206 function generator chip. The input frequency f2 is
compared against this reference that can be chosen with a switch from C
to B. There was a trimmer for every note in the even-tempered musical
scale. Even though the trimmers are low PPM (15 PPM/C) precision trimmers the
tuning wanders too much with temperature. I decided to replace the
XR2206 tuning reference with an top-octave-generator that is clocked
from a 2MHz crystal. FlatKeys (www.flatkeys.co.uk)
makes a replacement chip for the original MK50240 top octave divider.
Their FK50240 chip has 12 real synthesisers that tune from the master
clock to the desired notes, with a worst case error of 0.05 milliHertz
(0.00005 Hz). If you have a Polymoog or other 70s and 80s polyphonic
top-octave-generator based synthesiser you can change the tuning
accuracy to match the expectations of the 21st century with this
Flatkeys chip. Original MK50240 chips are also rare and difficult to
find so this is good news to keep those older instruments going.
Pictured is the FK50240 chip in its own plastic box and the old version
of this circuit.
Transistor VBE-matching circuit
Transistor VBE-matching circuit is ready and
working. Here is a picture of my measurement setup. The desk fan creates
a stream of room temperature air for transistors and the meter.
Transistors are moved with tweezers otherwise the finger-temperature
would ruin the measurements. I let the setup stabilise some 15-30
minutes before measurements. After the transistor is inserted to circuit
I wait also some 1-2 minutes until the voltage stabilises. With my
multimeter I can match the VBE to +/- 1mV. I hope this is enough. I read
that in original ARP-2600 the transistors were not matched at all so
this can not go wrong anyhow.
LFSR Noise
Soul of the Source of Uncertainty module is
alive ! In the picture LFSR-circuit is connected and is working. My
originally planned 17-bit LFSR-circuit didn't fit on this proto-board so
I changed it to 16-bit version (two 4015 shift-register
chips are enough for this). Length of this pseudo-random sequence is
2^16-1= 65535. If clocked with a 1Hz clock it repeats after 18 hours. I
recorded two sound examples of the serial output of this LFSR. First one
shows how it sounds when clock-rate sweeps from 0-34kHz. Second one
shows how good white noise this module can generate when clocked with
steady 34kHz. With this speed it should repeat after every 2s. If you
listen carefully with headphones you can hear it repeating. Now I can
connect the parallel output part of this circuit and check if my
probability potentiometers actually work.
http://1drv.ms/1tU57Ak
http://1drv.ms/1tU5hb6
http://1drv.ms/1tU57Ak
http://1drv.ms/1tU5hb6
MicroModular Buchla-simulation
I extended my pseudo random Nord Modular patch
with binary weighted pitch-generation. Now this patch simulates quite
well Buchlas Quantized Random Voltages output. With the switches in the
"Buffers and On/Off Switches"-section you can select
N from 1-6. "Binary Weighting" and "Summing" sections simulate the
final DA-conversion in Buchlas module. In patch there is also a switch
between the feedback loop from last shift register step to the beginning
of the LFSR. With this switch you can loop one 6-bit sequence from the
LFSR-stream. S/H slave-clock is created with 1ms positive edge delay
(see previous post). Pitch quantisation is done with the KeyQuant-module
before the output VCO. I tested different parallel output tap-positions
from the shift register but I think I will keep this original selection
(4,5,9,10,14,17). The "Binary Weighting"-section has much bigger effect
to the output than those different tap-positions. With 6-potentiometers
in the "Binary Weighting"-section you can modify the final random
voltage distribution as much as you like. Now I can proceed to build my
prototype of this module.
Nord Micromodular LFSR
I happen to be a owner of the Nord
Micromodular (the first G1 series). It is an extremely powerful modular
synthesiser in the size of a small book. Recently I have used it mainly
with my Akai EWI wind controller. Now I got an idea if I could
easily simulate different pseudo-random noise setups with Nord Modular
(see my first posting here). Micromodular has basic logic-modules but it
is too complicated to build shift registers from these primitive
building blocks. You can build shift registers by connecting serially
D-Flip Flops. A D-flip flop merely holds the value of its input when
the clock goes high. This is exactly what an S/H-module also does. You
connect serially as many S/H-modules as you need LFSR-stages and clock
them from a same master clock. In Micromodulars digital world we must
assure that the serially connected S/H-modules behave as a real
sequential storage element. This can be done with master-slave flip flop
design where there is a phase shift between clocks. Clock high is when
the master loads data and clock low when the slave transfers data to
the next stage. So you need two S/H-modules to one shift register stage.
This idea comes from Rob Hordijk and is explained in James J. Clarks
Nord Modular book (www.cim.mcgill.ca/~clark/nordmodularbook/nordmodularbook.pdf).
With this technique it is possible to build as long or as short LFSR-generators you want. In the picture you can see 17-stage pseudo-random noise generator patch. When it is clocked at 25kHz and the output comes from the shift registers last stage it generates fairly good white noise. It seems that you can go down to 6-stages and it generates still some kind of white noise. With this short LFSR you can hear the repeating of the generator. If you go down from 6-stages it generates pitches and you can use it as a VCO (or is it more like a DCO?). This looks and sounds promising. I think I must build a physical shift register module where you can patch your LFSR and explore more these short and repeating pseudo random sequences. There is sure a lot of to be discovered. When I have energy and time I must upload here some sound-examples of these sequences.
With this technique it is possible to build as long or as short LFSR-generators you want. In the picture you can see 17-stage pseudo-random noise generator patch. When it is clocked at 25kHz and the output comes from the shift registers last stage it generates fairly good white noise. It seems that you can go down to 6-stages and it generates still some kind of white noise. With this short LFSR you can hear the repeating of the generator. If you go down from 6-stages it generates pitches and you can use it as a VCO (or is it more like a DCO?). This looks and sounds promising. I think I must build a physical shift register module where you can patch your LFSR and explore more these short and repeating pseudo random sequences. There is sure a lot of to be discovered. When I have energy and time I must upload here some sound-examples of these sequences.
maanantai 8. joulukuuta 2014
TTSH 2600 Project
I have always wanted to own an ARP 2600
synthesiser. The prices for these monsters are insane high and what you
get with your money is a maybe-working old synth that you need to fix
now and then when the electronic components are at the end of their lives. So when I saw the Human Comparators (thehumancomparator.net)
ARP 2600 clone project (TTSH 2600) I immediately bought the panel and
PCB in the beginning of this year. I have gathered the components and
now I have the stuff and time to start building this. I started from the
three VCOs where I need matched NPN/PNP transistors. Ray Wilson from
MFOS (www.musicfromouterspace.com) has designed a tool for transistor matching. It is based on Robert Moogs original idea. Peter Kvitek from Midisizer (midisizer.com/other/vbe-matching)
has designed a nice PCB for this VBE-matching circuit. I converted
Peter's Eagle BRD-file to gerber-files that I sent to iTead Studio's PCB
prototyping service (imall.iteadstudio.com/open-pcb/pcb-prototyping.html).
This service is amazingly cheap. For this size PCB it was with the
shipping costs about 1.6€/PCB and the quality of the boards is very
good. One drawback in this service is that the minimum order quantity is
10 pcs (anybody there that would like to buy one ?). So now I must
first finish with this tool-building sub-project before I can continue
with my TTSH project.
Buchla Quantized Random Voltages
This is my first publication in this forum. I
have many ongoing DIY-projects and I will report about them here as they
proceed...
Buchla has a module called 266 Source of Uncertainty. It outputs random voltages with adjustable distribution probability. Doepfer has a really nice (and cheap) implementation of this module called A149. I started to build a prototype of my version of the quantized random voltages part of Buchlas module (picture shows the board with all the mechanical parts and potentiometers in place).
There is only one random voltage output but you can morph it from N+1 to 2^N states with six potentiometers. The potentiometer near the jacks adjusts N from 1 to 6.
Random voltages are generated with a 17-stage linear feedback shift register (LFSR) so the length of the sequence is 131071 states. If we clock this LFSR with 1Hz clock it starts to repeat after 36 hours. LFSR's are pseudo random not 100% random as is transistor created white noise. With a switch you can choose from 2 or 4 feedback tapping points (EXOR taps in LFSR). Buchla used also a 17-stage LFSR but the organisation of shift register was different and there was only one fixed feedback point. These differences can be described in terms of the amplitude distribution and the degree of low-pass filtering in the random voltages.
Bernie Hutchins from Electronotes has generously shared interesting articles about randomness, noise and LFSR's (EN#64,EN#76,EN#212,EN#402). These are freely downloadable from:
http://electronotes.netfirms.com/free.htm
Buchla has a module called 266 Source of Uncertainty. It outputs random voltages with adjustable distribution probability. Doepfer has a really nice (and cheap) implementation of this module called A149. I started to build a prototype of my version of the quantized random voltages part of Buchlas module (picture shows the board with all the mechanical parts and potentiometers in place).
There is only one random voltage output but you can morph it from N+1 to 2^N states with six potentiometers. The potentiometer near the jacks adjusts N from 1 to 6.
Random voltages are generated with a 17-stage linear feedback shift register (LFSR) so the length of the sequence is 131071 states. If we clock this LFSR with 1Hz clock it starts to repeat after 36 hours. LFSR's are pseudo random not 100% random as is transistor created white noise. With a switch you can choose from 2 or 4 feedback tapping points (EXOR taps in LFSR). Buchla used also a 17-stage LFSR but the organisation of shift register was different and there was only one fixed feedback point. These differences can be described in terms of the amplitude distribution and the degree of low-pass filtering in the random voltages.
Bernie Hutchins from Electronotes has generously shared interesting articles about randomness, noise and LFSR's (EN#64,EN#76,EN#212,EN#402). These are freely downloadable from:
http://electronotes.netfirms.com/free.htm
Tilaa:
Blogitekstit (Atom)